NumPy is one of the most powerful tools for working with probability distributions and other mathematical concepts in the Python programming language.
In this article, we'll take a look at some of the most commonly used probability distributions and laws in statistics and show you how to use NumPy to generate data and calculate probabilities.
Getting Started with NumPy
To get started with NumPy, you'll need to install the library using pip:
pip install numpyOnce you have NumPy installed, you can start working with probability distributions. Let's explore some of the probability laws.
The Normal Distribution
The normal distribution, also known as the Gaussian distribution, is a continuous probability distribution that is symmetric around the mean. It is often used to model real-world phenomena that exhibit a bell curves pattern, such as height or weight measurements.
Here's how you can generate random numbers from a normal distribution using NumPy:
import numpy as np
mu, sigma = 0, 0.1 # mean and standard deviation
s = np.random.normal(mu, sigma, 1000)
In this example, we're generating 1000 random numbers from a normal distribution with a mean of 0 and a standard deviation of 0.1.
Probability Density Functions
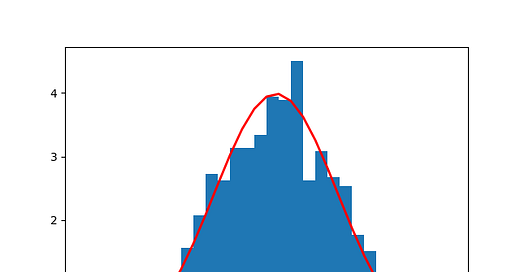
Once you have a set of random numbers, you can use NumPy to calculate the distribution's probability density function (PDF). The PDF describes the relative likelihood of a random variable taking on a certain value.
Here's an example of how to calculate the PDF of a normal distribution:
import matplotlib.pyplot as plt
count, bins, ignored = plt.hist(s, 30, density=True)
plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) *
np.exp( - (bins - mu)**2 / (2 * sigma**2) ),
linewidth=2, color='r')
plt.show()
This code generates a histogram of the random numbers we generated earlier, along with a plot of the PDF of the normal distribution. The PDF is calculated using the formula:
f(x) = (1 / (sigma * sqrt(2 * pi))) * exp(-(x - mu)^2 / (2 * sigma^2))
Other Probability Laws
Binomial Distribution
The binomial distribution models the probability of a certain number of successes in a fixed number of trials, where each trial has a fixed probability of success.
Here's an example of how to generate random numbers from a binomial distribution using NumPy:
n, p = 10, 0.5 # number of trials, probability of success
s = np.random.binomial(n, p, 1000)
You can also use NumPy to calculate the probability of a certain number of successes in a binomial distribution. For example, to calculate the probability of getting exactly 5 successes in 10 trials with a probability of success of 0.5, you can use the following code:
from scipy.stats import binom
n, p = 10, 0.5 # number of trials, probability of success
binom.pmf(5, n, p)This will output the probability of getting exactly 5 successes in 10 trials with a probability of success of 0.5, which is 0.24609375.
Poisson Distribution
The Poisson distribution models the probability of a certain number of events occurring in a fixed interval of time or space, where the events are rare and random, and the average rate of occurrence is known.
Here's an example of how to generate random numbers from a Poisson distribution using NumPy:
lam = 5 # average rate of occurrence
s = np.random.poisson(lam, 1000)You can also use NumPy to calculate the probability of a certain number of events occurring in a Poisson distribution. For example, to calculate the probability of getting exactly 3 events in an interval with an average rate of occurrence of 5, you can use the following code:
from scipy.stats import poisson
lam = 5 # average rate of occurrence
poisson.pmf(3, lam)This will output the probability of getting exactly 3 events in an interval with an average rate of occurrence of 5, which is 0.1403738958142805.
Exponential Distribution
The exponential distribution models the probability of a certain amount of time passing before a rare event occurs, where the event occurs randomly and independently of all other events.
Here's an example of how to generate random numbers from an exponential distribution using NumPy:
beta = 1 # rate parameter
s = np.random.exponential(beta, 1000)You can also use NumPy to calculate the probability of a certain amount of time passing before an event occurs in an exponential distribution. For example, to calculate the probability of waiting less than 1 unit of time before an event occurs with a rate parameter of 1, you can use the following code:
from scipy.stats import expon
beta = 1 # rate parameter
expon.cdf(1, scale=1/beta)
This will output the probability of waiting less than 1 unit of time before an event occurs with a rate parameter of 1, which is 0.6321205588285577.
De Morgan's Laws
De Morgan's Laws are rules that describe how to negate a logical expression involving two or more conditions. In probability theory, De Morgan's Laws can be used to calculate the probability of the complement of an event.
The first law states that the complement of the union of two events is equal to the intersection of their complements. In other words, the probability of either event A or event B occurring is equal to the probability of neither A nor B occurring:
P(A or B)' = P(A)' and P(B)'
Here's an example of how to use De Morgan's Laws to calculate the probability of the complement of a union of two events using NumPy:
# Generate random numbers from two different distributions
s1 = np.random.normal(0, 1, 1000)
s2 = np.random.normal(1, 1, 1000)
# Calculate the probability of either s1 or s2 being greater than 1
p1 = np.sum((s1 > 1) | (s2 > 1)) / 1000
# Calculate the probability of neither s1 nor s2 being greater than 1
p2 = np.sum((s1 <= 1) & (s2 <= 1)) / 1000
# Calculate the complement of the union of s1 and s2
p3 = 1 - p1
# Calculate the intersection of the complements of s1 and s2
p4 = 1 - p2
# Verify that the probabilities are equal
assert np.isclose(p3, p4)The second law of De Morgan's Laws states that the complement of the intersection of two events is equal to the union of their complements. In other words, the probability of both event A and event B occurring is equal to the probability of neither A nor B occurring:
P(A and B)' = P(A)' or P(B)'
Here's an example of how to use De Morgan's Laws to calculate the probability of the complement of an intersection of two events using NumPy:
# Generate random numbers from two different distributions
s1 = np.random.normal(0, 1, 1000)
s2 = np.random.normal(1, 1, 1000)
# Calculate the probability of both s1 and s2 being greater than 1
p1 = np.sum((s1 > 1) & (s2 > 1)) / 1000
# Calculate the probability of neither s1 nor s2 being greater than 1
p2 = np.sum((s1 <= 1) | (s2 <= 1)) / 1000
# Calculate the complement of the intersection of s1 and s2
p3 = 1 - p1
# Calculate the union of the complements of s1 and s2
p4 = 1 - p2
# Verify that the probabilities are equal
assert np.isclose(p3, p4)
Conclusion
Understanding probability theory is essential for anyone working with data, and being able to use Python and NumPy to work with probability distributions can be a powerful tool for data scientists and machine learning engineers.
That’s it for this issue. I hope you found this article interesting. Until next time!
Let’s connect :)